V této části si ukážeme, jak se bayesovské sítě dají využít při určování diagnózy pacienta a při testování znalostí studentů. Společným rysem těchto dvou aplikací je, že úloha odpovídá výpočtu podmíněných pravděpodobností u veličin, které nás zajímají – při znalosti hodnot pozorovaných veličin –, podmíněno veličinami, jejichž hodnoty jsme v konkrétním případě pozorovali.
V případě úlohy hledání diagnózy jsou veličinami našeho zájmu veličiny odpovídající daným diagnózám a pozorovanými veličinami jsou například výsledky provedených vyšetření, laboratorních testů apod. První rozsáhlou bayesovskou sítí aplikovanou v oblasti lékařství je síť nazývaná QMR-DT, což je zkratka pro Quick Medical Reference – Decision Theoretic Version. QMR byla vyvinuta v devadesátých letech minulého století a slouží k diagnostice onemocnění, s nimiž se internisté setkávají nejčastěji. Model obsahuje diagnostické veličiny, jako jsou anamnézy, příznaky a výsledky laboratorních testů, a veličiny odpovídající více jak 750 různým nemocem.
Vztahy mezi chorobami a příznaky jsou reprezentovány pomocí podmíněných pravděpodobností, které byly naučeny z dat amerického Národního centra pro zdravotnickou statistiku (National Center for Health Statistics). Struktura modelu odpovídá bipartitnímu grafu, v němž veličiny v horní vrstvě odpovídají nemocem a veličiny v dolní vrstvě odpovídají anamnézám, příznakům a výsledkům laboratorních testů. Model obsahuje pouze hrany vedoucí z veličin v horní vrstvě do souvisejících veličin v dolní vrstvě. V modelu nejsou žádné hrany mezi veličinami ve stejné vrstvě. To podle grafového kritéria pro podmíněnou nezávislost diskutovaného výše odpovídá předpokladu vzájemné nezávislosti anamnéz, příznaků a výsledků laboratorních testů při známé diagnóze. Obrázek 5 zobrazuje příklad struktury části QMR modelu.
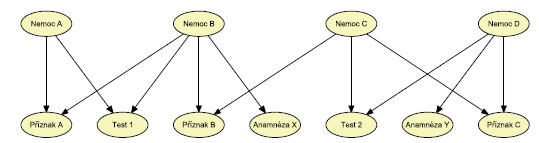
Obrázek 5
Příklad struktury části QMR modelu
Podobnou strukturu může mít i bayesovská síť, kterou lze využít pro testování znalostí studentů. Namísto nemocí se však v horní vrstvě objevují veličiny odpovídající testovaným dovednostem a v dolní vrstvě se objevují otázky použité při testování znalostí. Příkladem takového modelu je model bayesovské sítě pro státní maturitní test z matematiky v roce 2015. Tento model obsahuje 8 základních matematických dovedností a 26 matematických úloh, z nichž některé mají navíc ještě podúlohy, což dohromady vede na 37 veličin reprezentujících řešené úlohy. Dovednosti, které jsou pro řešení úloh třeba, jsou s touto úlohou spojeny hranou. K vytvoření struktury modelu byla využita expertní znalost autorů modelu, podmíněné pravděpodobnosti byly naučeny z dat shromážděných Centrem pro zjišťování výsledků vzdělávání (CERMAT). Příklad úlohy z maturitního testu z matematiky v roce 2015 je uveden na obrázku 6.

Obrázek 6
Příklad úlohy z maturitního testu z matematiky
Tento model byl využit pro tvorbu adaptivního testu znalostí, což je test, který nemá dopředu dané otázky, na něž musí testovaný student odpovědět. Otázky se vybírají v průběhu řešení testu na základě dosavadních odpovědí tak, aby přinesly co nejvíce informací o konkrétním studentovi. Zjednodušeně řečeno, pokud student zvládl složitější otázky, nebudeme se ho již ptát na lehké otázky, ale naopak na ty těžší. Nebo pokud vidíme, že správnými odpověďmi prokázal, že má některé potřebné dovednosti, zaměříme se na jiné schopnosti, ve kterých panuje ještě nejistota. Takovéto adaptivní testy je třeba provádět na počítači, a spíše než by nahradily maturitní testy, mohou posloužit studentům při přípravě na maturitu. Pro výběr otázky, která bude položena, se využije z bayesovské sítě získaná podmíněná pravděpodobnost pro dovednosti, kdy podmiňujeme dosavadními odpověďmi studenta. Vhodným kritériem výběru je pak například minimalizace očekávané entropie pravděpodobnostní tabulky dovedností.
Jiným příkladem bayesovské sítě pro testování znalostí je diagnostický model studentů řešících aritmetické úlohy se zlomky. Tento model byl publikován v roce 2004. Od předchozího modelu se liší v tom, že obsahuje nejen dovednosti potřebné pro řešení úloh se zlomky, ale i typické špatné návyky při řešení úloh se zlomky. Navíc model také obsahuje veličiny, které odpovídají schopnosti aplikovat získané dovednosti v konkrétním úkolu. V modelu jsou také zahrnuty pozorované závislosti mezi těmito veličinami. Toto bylo možné díky detailní analýze pracovních listů s řešením úloh, díky níž byly zaznamenávány pozorované dovednosti, špatné postupy atd. Tvorba takového modelu je výrazně pracnější, ale umožňuje jeho použití i pro detailní diagnostiku dovedností a špatných postupů testovaných studentů. Struktura modelu je na obrázku 7. Hnědě podbarvené veličiny odpovídají skrytým (nepozorovaným) veličinám, modře podbarvené dovednostem, červené špatným postupům a světle žluté jednotlivým úlohám.
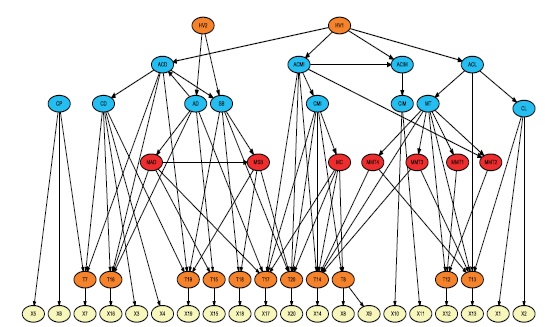
Obrázek 7
Diagnostický model studentů řešících aritmetické úlohy se zlomky
úryvek z knihy:
Jiří Vomlel: Bayesovské sítě
Academia 2024
O knize na stránkách vydavatele

 Sciencemag.cz
Sciencemag.cz




