Představme si, že na kraji stolu vytváříme hromadu z obdélníkových destiček, přičemž klademe jednu na druhou, aby sloupec co nejvíce přesahoval přes okraj.
Jestliže má každá destička délku 1 (v libovolných jednotkách), jak velký převis můžeme vytvořit, aniž se celá konstrukce působením gravitace zhroutí? Máme-li jen jednu destičku, pak zmíněný přesah bude zřejmě roven 1/2 délkové jednotky. Se čtyřmi destičkami se ale vyšplháme až k převisu délky

což již o něco přesahuje jedničku, takže svrchní destička se bude celá vznášet mimo stůl.
Chceme-li dosáhnout převisu delšího než dvě délkové jednotky, bude nám stačit 31 destiček. S 31 destičkami totiž maximální možný převis činí

A takto lze pokračovat s maximálním možným převisem činícím
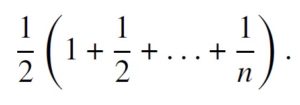
Poněkud překvapivě lze takto dojít k závěru, že převis můžeme vyrobit libovolně velký, máme-li k dispozici dostatečné množství destiček, protože nekonečná řada
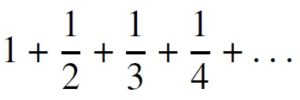
diverguje, tedy nemá konečný součet.
Musím se ale přiznat, že jsem dlouho podceňoval, jak pomalu tato řada diverguje, dokud jsem se neocitl na matematickém představení s hromadou krabic od pizzy ve velkém divadle v centru města.
Před začátkem představení jsem čistě ze zvědavosti vypočítal, jak vysoký by musel být sloupec vytvořený z krabic k tomu, aby konstrukce vytvořila převis přes pódium.
Odpověd’zněla 5,8 světelného roku.
Tento text je úryvkem z knihy
David Acheson: Kalkulus a jeho dobrodružství
Matematika pro odvážné
Dokořán 2024
O knize na stránkách vydavatele

 Sciencemag.cz
Sciencemag.cz





