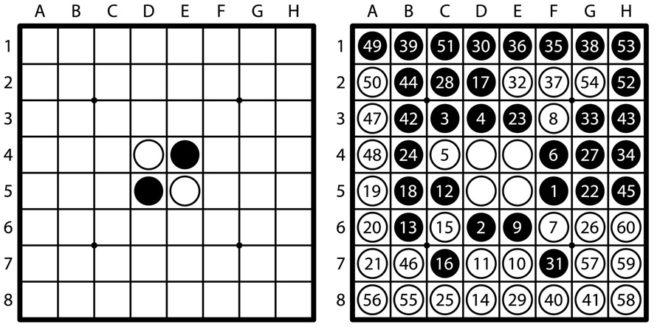
Othello (Reversi) je desková hra populární dnes především v Japonsku. Vznikla ovšem na konci 19. století v Anglii a její název se skutečně odvozuje od Shakespearova díla. Hraje v ní bílý proti černému na desce o rozměrech šachovnice (obdobná je pak i notace, viz obrázek), ovšem použité kameny mohou měnit barvu (obracejí se, když jsou „obklíčeny/zajaty“; tím hra zase trochu připomíná Go).
Japonský bioinformatik Hirokiho Takizawy nyní oznámil, že hra byla „vyřešena“ v tom smyslu, že se podařilo najít optimální strategii za obě strany. Jde o tzv. slabé řešení, kdy použitý algoritmus zajistí buď výhru, nebo remízu – ze základní pozice. Algoritmus není postaven tak, aby dokázal najít nejlepší pokračování z libovolné pozice (PH: tj. pokud některý z hráčů nebude pokračovat optimálně, druhá strana bude mít postačující strategii; ale analyzovány nejsou pozice, které by vznikly chybnou hrou obou stran – tak tomu alespoň rozumím). Těch má být mimochodem asi oktilion (10 na 48).
H. Takizawa využil superpočítačový klastr MN-J. Dále rozšířil program Edax, který byl před lety poprvé použit k analýze strategie Othello. K průlomu došlo podle něj především díky zlepšení efektivity vyhledávání.
Hiroki Takizawa, Othello is Solved, arXiv (2023). DOI: 10.48550/arxiv.2310.19387
Zdroj: arXiv/TechXplore.com
Poznámky PH:
Jak to chápu, řešení bylo provedeno prostě hrubou silou. Se vším, co se vztahuje k počítačově prováděným matematickým důkazům.
Výsledek na konci (viz obrázek) je skutečně 32 kamenů bílého i černého.
Přichází u této hry v úvahu „nevýhoda tahu“? Asi ne, spíš je vždycky výhodnější táhnout, a tedy i začínat… (tj. v úvahu přicházely pouze dva možné výsledky při oboustranně optimální hře?)
 Sciencemag.cz
Sciencemag.cz




U teto hry je nevyhoda tahu podstatna. Kdysi na staricke Nokii jsem nasel postup na absolutni vitezstvi (vsechny kameny byly me) a v podstate od asi dvacateho tahu mel telefon vzdy jen jeden mozny tah, kterym mi pripravil kameny k zajmuti. Samozrejme ten ppostup fungoval jen na konkretni verzi te hry.
a nebo je rozhodovani o dalsim optimalnim kroku v tak uzkem
udoli moznosti, ze se strom moznosti nema sanci moc rozvetvit
a jde to hrubou silou. tipuju, ze rozumnych tahu neni moc v kazdem kole, tak 2 az 4.
dekuji za upresneni, priznam se, ze jsem tu hru nikdy nehral. ani nevim, ze ma vice verzi, respektive tomu nerozumim…