Jedna z verzí známé úlohy obchodního cestujícího. Jak propojit několik měst sítí silnic tak, aby byla jejich délka co nejkratší?
Pro ilustraci obtížnosti této úlohy se podívejme na „snadný“ případ, kdy máme propojit pouhá čtyři města A, B, C, D, která navíc šťastnou náhodou leží ve vrcholech čtverce o straně 1.
Jediným požadavkem je, aby se obyvatelé kteréhokoli ze čtyř měst mohli po silnici dostat do libovolného jiného města. Naše síť může tedy sestávat například ze tří úseček:
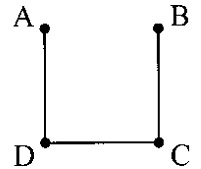
Avšak tato síť o celkové délce tří délkových jednotek rozhodně není nejkratší. Po chvíli zkoušení přijdeme na to, že dvě úhlopříčky, protínající se ve středu čtverce, tvoří kratší síť:
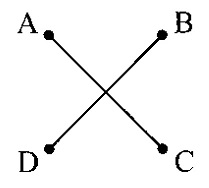
Každá z úhlopříček totiž měří podle Pythagorovy věty √2 délkových jednotek, takže celková délka sítě je 2√2 = 2,83, což je méně než 3.
Pochopitelně se ihned nabízí otázka, zda bychom mohli zkonstruovat jinou, ještě o něco kratší síť, kdybychom povolili více průsečíků. Dejme tomu, ale kolik jich máme povolit a kam je máme umístit?
To jsou velice těžké úlohy. Jeden ze způsobů, jak na ně, je podvádět a využít mýdlových bublin.
Vezmeme dvě desky z průhledného plexiskla propojené čtyřmi kolíky umístěnými do vrcholů čtverce. Ponoříme-li toto zařízení do mísy s mýdlovou vodou a zase je vytáhneme, dostaneme mýdlovou blánu s povrchem menším, než by měl jakýkoli jiný tvar byť jen málo odlišný. Jinými slovy, dostáváme vážného kandidáta na řešení našeho problému optimální silniční sítě.
A dříve nebo později obdržíme mýdlovou blánu opravdu svérázného tvaru:

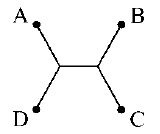
Ačkoli matematický důkaz nepatří k nejsnazším, toto je skutečně hledané řešení našeho problému silniční sítě: pět úseček se dvěma průsečíky tří z nich pod úhlem 120°. Celková délka této sítě činí 1 + √3 = 2,73 jednotek a žádná kratší síť neexistuje.
Tento text je úryvkem z knihy
David Acheson: 1089 a další parádní čísla. Matematická dobrodružství
nové vydání Dokořán 2023
O knize na stránkách vydavatele

 Sciencemag.cz
Sciencemag.cz




