Sciencemag.cz
Doporučujeme
NP úplné problémy představují výzvu. Jejich složitost (doba potřebná k řešení) roste s délkou vstupu exponenciálně (nebo alespoň neznáme efektivnější algoritmy). Vědci proto zkoumají alternativy k tradičním výpočetním metodám; optické počítače (nebo optické analogové systémy) představují jednu z možností.
Na čínské Shanghai Jiao Tong University nyní vyvinuli rekonfigurovatelný trojrozměrný integrovaný fotonický procesor speciálně navržený pro řešení problému součtu podmnožin (SSP, subset sum problem), což je klasický NP úplný problém. Jako subset sum se označuje úloha, kdy je na jedné straně zadána množina přirozených čísel, na druhé straně (větší) přirozené číslo. Ptáme se, zda v původní množině existuje podmnožina, jejíž součet dá dané číslo.
Viz také: Fotonický počítač efektivně řeší NP úplný problém
Zvolenou technikou byl přímý zápis femtosekundovým laserem. Výzkumníci zkonstruovali fotonický čip složený z 1 449 standardizovaných optických komponent. Tato technologie umožňuje rychlou tvorbu prototypů a nabízí větší flexibilitu návrhu, která je pro řešení složitého problému SSP klíčová.
Mapováním tohoto problému na fotonický procesor mohou výzkumníci zakódovat chování světla k provádění výpočtů. Procesor funguje tak, že umožňuje fotonům ve světelném paprsku prozkoumat všechny možné cesty současně a paralelně poskytovat odpovědi. Tato konstrukce nejen urychluje výpočet, ale také zachovává vysokou přesnost – což dokládá schopnost procesoru řešit různé instance SSP se stoprocentní spolehlivostí.
Možnosti využití této technologie přesahují problém součtu podmnožin. Rekonfigurovatelnost procesoru by mohla být přizpůsobena pro úlohy, jako jsou optické neuronové sítě a fotonické kvantové výpočty.
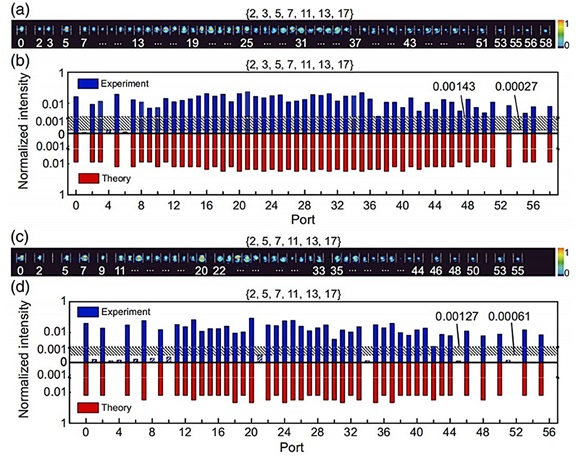
Výsledky výpočtů instancí SSP, kde je množina {2, 3, 5, 7, 11, 13, 17} a {2, 5, 7, 11, 13, 17}. (a) a (c) Experimentální odečet se zobrazí jako řada skvrn, které potvrzují existenci příslušných součtů podmnožiny (tj. čísel pod skvrnami). (b) a (d) Experimentální a teoretické rozložení intenzity. V teoretických případech nenulová intenzita potvrzuje existenci součtu podmnožiny. Použitím přiměřeného prahu intenzity lze experimentální signály správně klasifikovat na platné (za prahem) a neplatné (pod prahem). Toleranční intervaly prahových hodnot jsou vyznačeny černými pásy. Kredit: Advanced Photonics (2024). DOI: 10.1117/1.AP.6.5.056011
Xiao-Yun Xu et al, Reconfigurable integrated photonic processor for NP-complete problems, Advanced Photonics (2024). DOI: 10.1117/1.AP.6.5.056011
Zdroj: SPIE / TechXplore.com
