Tag Archives: geometrie

Společnost OpenAI se pochlubila, že jeden z jejích interních modelů umělé inteligence našel protipříklad ke slavné domněnce, kterou v roce 1946 vyslovil legendární maďarský matematik Paul Erdős. Erdős je samozřejmě populární postavou, viz už koncept Erdősova čísla. I mezi nematematiky je znám svými výstřednostmi nebo zálibou v amfetaminech. Problém jednotkové …

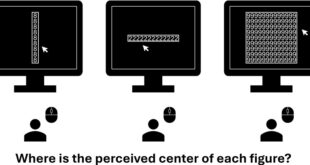
Když byl pruh pokryt menšími čísly, ukázalo se, že dobrovolníci systematicky umisťovali střed více doleva než u větších čísel. Vědci z Tokijské metropolitní univerzity studovali vztah mezi numerickými informacemi v našem zraku a tím, jak ovlivňují naše vnímání prostoru. Dobrovolníci byli požádáni, aby určili střed čar a čtverců vyplněných čísly; …

Co nám dokáže říct moderní informatika o starověkých tělesech? Na takovou otázku se zaměřil Jan Hartman ve své bakalářské práci věnované barvení platónských a archimédovských těles. Absolvent v ní zkombinoval klasický problém a moderní metody vizualizace, a otevřel tak nové perspektivy v obou oblastech. Představte nám, čemu jste se ve své práci věnoval? Ve své práci …

Vědci chtěli po modelu ChatGPT verze 4, aby vyřešil problém probíraný již v antice – zdvojnásobení (obsahu) čtverce, tj. jak dlouhou stranu má být větší druhý čtverec. Výsledky byly nečekané. Řekové k těmto problémům přistupovali primárně geometricky. Otázkou se zabýval podrobně Platon (vložil vše jako obvykle do úst Sokratovi) v …

Revoluční teorie trojrozměrného času od Günthera Kletetschky z Ústavu hydrogeologie, inženýrské geologie a užité geofyziky Přírodovědecké fakulty Univerzity Karlovy představuje elektrický náboj jako topologickou vlastnost časového prostoru. Tento přístup umožňuje vysvětlit kvantování náboje i jeho konzervaci z čistě geometrické perspektivy. V nejnovějších pracích publikovaných v tomto roce Güntherem Kletetschkou, je …

Jak vyplývá ze speciální teorie relativity, objekt pohybující se rychlostí blízkou rychlosti světla má (pro pozorovatele) jinou délku, než když je v klidu, a čas pro něj plyne jinak než v laboratoři. To vše bylo opakovaně potvrzeno experimenty. Jeden zajímavý důsledek teorie relativity však dosud pozorován nebyl – takzvaný Terrell-Penroseův …

Fyzikové vytvořili první dvojrozměrnou verzi Boseho skla, nové fáze hmoty, která údajně „zpochybňuje statistickou mechaniku“. Boseho sklo má některé vlastnosti skla a všechny částice jsou v něm lokalizovány. To znamená, že žádná částice v systému se nemísí se svými sousedy. Kdyby byla káva lokalizovaná, pak by při míchání mléka do …

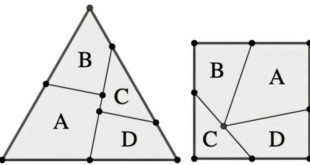
Henry Ernest Dudeney (1857-1930) byl anglický matematik a specialista na rekreační matematiku/matematické hry a hlavolamy. V roce 1907 přišel s problémem, jak libovolný rovnostranný trojúhelník rozřezat na co nejmenší počet dílků, aby jejich přeuspořádáním vznikl čtverec. Sám Dudeney následně přeložil řešení, že to vždy lze provést rozdělením na 4 díly …

Pochopení toho, jak se formují a vyvíjejí přepravní sítě, například říční systémy, je klíčové pro optimalizaci jejich stability a odolnosti. Sítě v závislosti na svém typu nejsou stejné. Stromovité struktury jsou vhodné pro přepravu, zatímco sítě obsahující smyčky jsou odolnější vůči poškození. Jaké podmínky podporují vznik smyček? Na tuto otázku …

Víme, že jezdec se může pohybovat po šachovnici rychleji než král, ale jak je to přesně? Matematik Christian Táfula Santos z University of Montreal to spočítal. Jeho důkaz byl zveřejněn na preprintovém serveru arXiv (tj. prozatím bez odborné recenze/oponentury). Závěr zní, že jezdec může dosáhnout svého cíle v průměru 24/13krát, …