Foton může projít současně dvěma štěrbinami, ale kupodivu už ne třemi.
Známý dvouštěrbinový experiment se nachází v samém jádru kvantové mechaniky. Schopnost fotonu projít v určitém ohledu „oběma štěrbinami současně“ byla již diskutována opakovaně, včetně závislosti výsledků na konkrétním uspořádání pokusu.
Fyzikové z Vídeňské technické univerzity a Rakouské akademie věd se ovšem zaměřili na otázku, proč by foton nemohl projít současně ještě větším počtem štěrbin. Třemi? Čtyřmi? Kupodivu to tak nefunguje, jako kdyby u dvou existoval nějaký limit – částice nelze současně delokalizovat na více než dvou místech. Interferenční vzorce, které dostaneme u více štěrbin, se dají popsat tak, jako by částice prošla současně právě dvěma z nich. Máme matematický aparát, který situaci dobře popisuje a teorie dokáže správně předpovědět, jak který pokus s více štěrbinami dopadne, ale pochopitelné to není už prakticky vůbec. A navíc logicky vzniká otázka – má příslušný limit nějakou fundamentální fyzikální příčinu?
Jenom pro určitou představu zkusili autoři několika prací na toto téma celý problém „přeložit“, tedy popsat ekvivalentním způsobem jako kooperativní hru, kdy namísto chápání interference jde o informaci. V téhle podobě je celá věc pro náš rozum prý mnohem přístupnější (poznámka PH: akorát musíme uvěřit tomu, že zde skutečně platí ekvivalence).
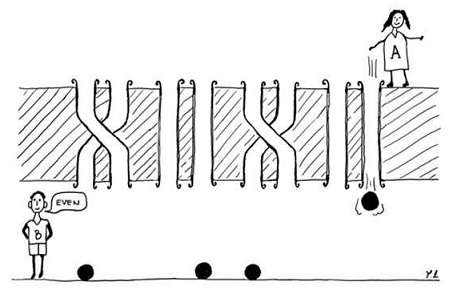
Credit: © Borivoje Dakić
Jak ukazuje obrázek, před sebou máme štěrbiny, respektive kanály. Některé z dvojic jsou v oddělující zdi překřížené. Na jednom konci systému se nachází Alice, na druhém Bob. Jejich cílem je zjistit, jak celé propojení vypadá, a to s použitím co nejmenšího množství částic/pokusů. Jak na to? Oba se např. dohodnou, že Alice hodí kuličku vždycky do pravé trubky z každého páru. Z toho, kde kulička vypadne, se zjistí, kolik/které páry trubek jsou rovné a které se ve zdi kříží. V klasické světě nelze získat úplnou informaci („vyhrát hru“) s použitím méně kuliček, než je párů trubek.
Naopak v kvantové fyzice může kulička procházet dvěma štěrbinami současně. Dvě kvantové kuličky dokáží napodobit chování 4 obyčejných. K získání informace nám postačí 2 kvantové kuličky, respektive obecně polovina páru trubek/čtvrtina trubek. A teď si představme hru, kdy kulička může procházet ještě více štěrbinami současně – z toho vždy zase může spočítat potřebný počet kuliček v závislosti na jejich vlastnostech.
Ve fyzikální realitě nicméně kdovíproč máme jen ekvivalenty kuliček klasických a kvantových, které procházejí dvěma štěrbinami, hru nevyhrajeme s menším počtem tahů. To jsme tedy věděli už předtím, nicméně představit si situaci jako tuto hru má pro povahu kvantové superpozice údajně poskytovat intuitivnější rámec pro další zkoumání než přemítat o tom, jak vlnočásticích a interferenci.
Sebastian Horvat et al. Interference as an information-theoretic game, Quantum (2021). DOI: 10.22331/q-2021-03-08-404
Sorkin, Rafael D. „Quantum mechanics as quantum measure theory.“ Modern Physics Letters A 9.33 (1994): 3119-3127)
Nicolas Brunner et al. Publisher’s Note: Bell nonlocality [Rev. Mod. Phys.86, 419 (2014)], Reviews of Modern Physics (2014). DOI: 10.1103/RevModPhys.86.839
Zdroj: Borivoje Dakic & Sebastian Horvat, University of Vienna / Phys.org
Poznámka PH: V tiskové zprávě se přesněji řečeno nemluví o tom, že by nás zajímal nutně samotný počet překřížení, ale to, zda je počet lichý, nebo sudý. Jaký to má smysl / jaký je v tom rozdíl? (I kdyby kvantová kulička dokázala pouze říct, ve 4 trubkách je jedno křížení – ale ne u které z dvojic – stejně tím dostáváme absolutní čísla.)
 Sciencemag.cz
Sciencemag.cz





