Archiv článků: geometrie

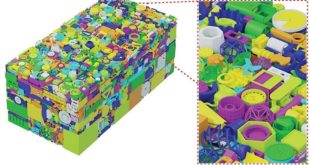
Jak optimálně uspořádat v prostoru určitý počet koulí? Tento problém má za sebou dlouhou historii. Už Kepler vyslovil domněnku, že nejhustším uspořádáním pro nekonečný počet koulí je struktura FCC (face-centered cubic), podobná hexagonálnímu uspořádání pomerančů a jablek, které můžeme vidět v supermarketech. Máme-li konečný počet koulí, všechno se ale komplikuje; …

Už Kepler si položil otázku, jak můžeme koulemi co nejhustěji vyplnit daný prostor (typicky krabici). Řešením je krychlová mřížka, kdy koule v další vrstev dáváme do středu mezi čtyřmi pod nimi. Kepler toto řešení navrhl, ale trvalo ještě přes 400 let, než se podařilo dokázat, že jde opravdu o nejefektivnější …

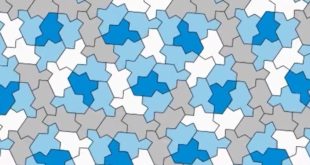
Neperiodická dláždění představují oblíbené téma v populárních knihách o matematice, zabývají se jimi profesionální matematici i laičtí zájemci. Nedávno byl objeven objekt zvaný einstein („jediný kámen“, tj. vystačíme s jedinou dlaždicí, nepotřebujeme kombinaci více tvarů), tedy mnohoúhelník, jimž lze rovinu pokrýt. Viz také: Matematici objevili neperiodické dláždění roviny jedinou dlaždicí …

Každý mořeplavec vám řekne, že nejkratší vzdálenost mezi dvěma body na povrchu koule je úsek hlavní kružnice. Promítneme-li hrany mnohostěnu na kulovou plochu jemu opsanou, vznikne množina oblouků hlavních kružnic zvaná radiální projekce. V levém sloupci na protější straně jsou znázorněny radiální projekce platónských těles. Tečkovaně jsou vyznačeny příslušné hlavní …

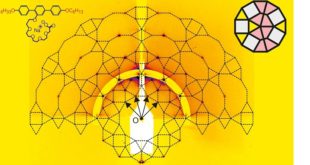
Kvazikrystaly mají pravidelnou strukturu podobnou normálním krystalům, avšak v případě kvazikrystalů do sebe základní jednotky dokonale „periodicky“ nezapadají. Výsledkem jsou zvláštní vlastnosti, pro určité technologické aplikace třeba i výhodnější. Nově objevený kapalný kvazikrystal se skládá z dvanáctiúhelníků, které jsou samy tvořeny kombinací trojúhelníkových, čtvercových a poprvé i lichoběžníkových buněk. „Objevili …

Grafit/grafen a fullereny představují modifikace uhlíku s hybridizací sp2, kdy je každý atom uhlíku navázán na tři sousední. Grafen má přitom nulovou křivost, fullereny kladnou (kulovou), kdy se stáčejí dovnitř. Nemohla by existovat i forma uhlíku se zápornou křivostí, hyperbolickou, „rozbíhající se od sebe“? Příslušné geometrie se probírají např. v …

Některými mnohoúhelníky lze rovinu vyskládat beze zbytku, jinými ne. Stejně tak můžeme zkoušet rovinu pokrýt kombinací útvarů různých. Zajímavé to začne být v případě dláždění tzv. neperiodických. V populární literatuře se toto téma těší pozornosti pravděpodobně hlavně proto, že s touto myšlenkou přišel už celkem dávno Hawkingův spolupracovník a nositel …

Chemici a nanotechnologové dnes dokážou věci zdánlivě nemožné. Známá Möbiova páska, populární ve sci-fi nebo i v kosmologických apod. úvahách, by se dala chápat vlastně jako extrémně krátká uhlíková nanotrubička, rozstřihnutá, přetočená a zase slepená. Úžasné je, že co člověk provede s papírem pomocí nůžek a lepidla, dnes chemici a …

Objevit nejjednodušší a nejefektivnější způsob, jak v daném prostoru vyrovnat na kupu pomeranče, je jedním z těch zdánlivě prostě znějících úkolů, jež mají dalekosáhlé matematické důsledky. Nejjednodušší způsob, jak vyrovnat kulovité předměty, představuje trojúhelníkové nebo čtvercové uspořádání (1–3); tyto konfigurace zjevně souvisí s pravidelným rozdělením roviny. Když se první vrstva …

…nakonec idea čtvrtého rozměru překročila Atlantik a dorazila do Ameriky. Jejím poslem byl barvitý anglický matematik jménem Charles Howard Hinton. V době, kdy Albert Einstein úřadoval na švýcarském patentovém úřadě, pracoval Hinton pro patentový úřad Spojených států ve Washingtonu. Ačkoli se pravděpodobně nikdy nesetkali, zkřížily se jejich cesty několika zajímavými …