…nakonec idea čtvrtého rozměru překročila Atlantik a dorazila do Ameriky. Jejím poslem byl barvitý anglický matematik jménem Charles Howard Hinton. V době, kdy Albert Einstein úřadoval na švýcarském patentovém úřadě, pracoval Hinton pro patentový úřad Spojených států ve Washingtonu. Ačkoli se pravděpodobně nikdy nesetkali, zkřížily se jejich cesty několika zajímavými …
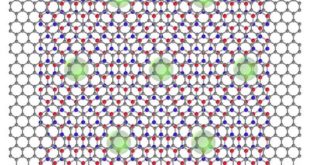
více »Viry jako šablona pro nanotechnologie vedly k tvorbě antiferomagnetu
Viry vytvářejí různé geometricky pravidelné struktury, daly by se proto využívat k pěstování dalších materiálů jako lešení – v tomto případě nám nejde o jejich biologické funkce, takže bychom používali viry nějak inaktivní (alespoň vzhledem k člověku). V časopisu Journal of Polymer Science byla publikována studie výzkumníků z University of …
více »Městem chodíme neefektivně, nejkratší cestu nenajdeme
Nejkratší vzdálenost mezi dvěma body je přímka. Při chůzi po městských ulicích nebo konec konců i v terénu však přímá linie nemusí být možná. Jak se rozhodujeme, kudy jít? Nová studie MIT naznačuje, že náš mozek ve skutečnosti není optimalizován pro výpočet nejkratší cesty. Na základě souboru dat více než …
více »Kruhy, mé kruhy
Kruh a kruhový pohyb znamenají popření moci času. Proto nikterak nevadí, že kruhům tolik času věnuji, protože při péči o kruhy mi ho neubývá. Geometrická minipovídka. Kruhy, mé kruhy. Prakticky veškerý čas mi zabírá péče o kruhy, jejich náležité vytváření, udržování, související drobné úpravy a samozřejmě též rozšiřování. Kruhy jsou …
více »Tabulka Si.427 má ukazovat zrod babylónské trigonometrie
Babyloňané, jak známo, znali Pythagorovu větu. Tabulka z doby asi 1700 př. n. l. (starobabylonské období) má představovat nejstarší důkaz nejen této znalosti, ale i babylonské goniometrie obecně. Tisková zpráva k příslušné studii mluví o „aplikované geometrii“ a „protogoniometrii“. Tedy nám (laikům) by to asi nepřipadalo jako goniometrie, protože toto …
více »Mandelbrotova mapa
Když se z matematiky stává čisté umění… Když v roce 1982 Benoit B. Mandelbrot vydal knihu The Fractal Geometry of Nature (Fraktální geometrie přírody), brzy každý, kdo měl osobní počítač (včetně mě), začal psát jednoduché programy pro zobrazování Juliových množin, kapradí a mraků. (Není známo, co znamená zkratka B. v …
více »Dokázali Kellerovu domněnku pro 7 dimenzí
90 let starý problém z oblasti geometrie padl díky speciálnímu nasazení algoritmu, který převedl matematickou otázku na problém splnitelnosti. Kellerova domněnka spadá do kategorie populárních problémů dláždění. Otázka zní, zda rovinu můžeme pokrýt jedním typem dlaždic, aniž by se překrývaly jejich hrany (viz obrázek pro čtverce; jindy se problém formuluje …
více »Podivné koule v 7D
V sedmirozměrném světě existují objekty podobající se koulím, ovšem s drobnou odlišností. Normální koule, ať už ve 3D nebo v 7D (nebo podobně i kruh ve 2D), se skládá ze 2 polokoulí, které prostě dáme k sobě. V 7D ale takové polokoule můžeme k sobě připojit (formálně zřejmě nějak jako: …
více »Einstein by se asi divil: Lorenztova geometrie popisuje a optimalizuje nástup do letadel
Vědci využili skutečně kuriózní metodu pro popis nástupu lidí do letadel – docela se prý hodí aplikovat matematiku z obecné teorie relativity. Jméno Lorentz známe především v souvislosti s příslušnou transformací, pomocí které se ve speciální teorii relativity přepočítávají při rychlostech blízkých rychlosti světla délky, časy a hmotnosti. (Příslušná matematika …
více »Démoni z Escherova obrazu odpovídají deformacím krystalů
Fascinující obrazy nizozemského malíře M. C. Eschera inspirují matematiky i fyziky od svého vzniku. Escherova díla souvisejí s takovými obory, jako je krystalografie či hyperbolická geometrie. Kresba Circle Limit IV (Heaven and Hell) představuje mozaikování pomocí obrazů andělů a démonů, které vyplňují kruh bez prázdných mezer. Paolo Biscari a jeho …
více » Sciencemag.cz
Sciencemag.cz