Už Kepler si položil otázku, jak můžeme koulemi co nejhustěji vyplnit daný prostor (typicky krabici). Řešením je krychlová mřížka, kdy koule v další vrstev dáváme do středu mezi čtyřmi pod nimi. Kepler toto řešení navrhl, ale trvalo ještě přes 400 let, než se podařilo dokázat, že jde opravdu o nejefektivnější …
více »Za hranice dat: imputace
Přirozeným návrhem, jak se vypořádat s neúplnými údaji, je doplnit je vložením náhrad za chybějící hodnoty. Tato strategie se nazývá imputace. Protože díky ní jsou data úplná, po imputování chybějících hodnot se nemusíme starat o žádné mezery a můžeme pokračovat v analýze dat jakýmkoli způsobem. Například po doplnění hodnot za …
více »Mimozemské řeky pod lupou: Proč na Titanu skoro chybí delty?
Řeky tečou (tekly) kromě Země ještě minimálně na dalších dvou světech Sluneční soustavy: na Marsu a na Titanu, kde jsou tvořeny kapalným metanem. Nová technika vyvinutá geology z MITu a dalších institucí umožňuje mimozemské řeky podrobněji analyzovat. Metoda využívá satelitní pozorování k odhadu rychlosti, jakou řeky přemísťují tekutinu a sedimenty. …
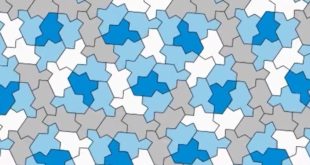
více »Neperiodické dláždění roviny jedinou dlaždicí: příběh má pokračování
Neperiodická dláždění představují oblíbené téma v populárních knihách o matematice, zabývají se jimi profesionální matematici i laičtí zájemci. Nedávno byl objeven objekt zvaný einstein („jediný kámen“, tj. vystačíme s jedinou dlaždicí, nepotřebujeme kombinaci více tvarů), tedy mnohoúhelník, jimž lze rovinu pokrýt. Viz také: Matematici objevili neperiodické dláždění roviny jedinou dlaždicí …
více »Matematik z Matfyzu získal Gödelovu cenu za problém obchodního cestujícího
Autorovi jsme položili několik otázek týkajících se toho, nakolik má řešení úlohy obchodního cestujícího pomocí lineárního programování vztah problému P vs. NP, v současnosti jednomu z hlavních otevřených matematických problémů. Clayův matematický ústav za jejich řešení nabízí milion dolarů. Nejprve tisková zpráva Matematicko-fyzikální fakulty UK Na Matfyz putuje jedno z …
více »Vedlejší kružnice
Každý mořeplavec vám řekne, že nejkratší vzdálenost mezi dvěma body na povrchu koule je úsek hlavní kružnice. Promítneme-li hrany mnohostěnu na kulovou plochu jemu opsanou, vznikne množina oblouků hlavních kružnic zvaná radiální projekce. V levém sloupci na protější straně jsou znázorněny radiální projekce platónských těles. Tečkovaně jsou vyznačeny příslušné hlavní …
více »Sebevědomí, nesoudní, nekompetentní: Dunningův–Krugerův efekt byl zpochybněn
Dunningův–Krugerův efekt je označení pro neschopnost vyhodnotit objektivně vlastní neschopnost :-). Čím méně kompetentní v daném oboru (apod.) člověk je, tím spíše bude sám sebe přeceňovat, např. při odhadu úspěšnosti v nějakém testu. Populárně řečeno, když je někdo opravdu blb, pak k k tomu patří, aby si ani neuvědomoval, že …
více »Složité matematické modely ve sportu zatím nedominují
Dnešní digitální technologie umožňují získat o sportovních utkáních obrovské množství informací. Zdaleka nejde jen o samotný výsledek. Zůstaneme-li u her typu fotbalu a hokeje, pak vedle gólů třeba zjistíme, kdo po většinu času držel míč, na jaké polovině se převážně hrálo, kolik střel směřovalo na bránu, jaký měly „koeficient“ (pravděpodobnost, …
více »Kvantový systém dokáže rozpoznávat prvočísla
Nová studie slibuje analýzu čísel fyzikálními metodami, pomocí jakéhosi analogového počítače. Tímto způsobem by mělo jít rozhodnout třeba o tom, zda je nějaké obří číslo prvočíslem (nebo zda patří do nějaké jiné speciální skupiny, průvodní tisková zpráva zmiňuje např. šťastná čísla). Autoři studie pomocí holografických laserových technik vytvořili systém s …
více »Matematici objevili neperiodické dláždění roviny jedinou dlaždicí
Některými mnohoúhelníky lze rovinu vyskládat beze zbytku, jinými ne. Stejně tak můžeme zkoušet rovinu pokrýt kombinací útvarů různých. Zajímavé to začne být v případě dláždění tzv. neperiodických. V populární literatuře se toto téma těší pozornosti pravděpodobně hlavně proto, že s touto myšlenkou přišel už celkem dávno Hawkingův spolupracovník a nositel …
více » Sciencemag.cz
Sciencemag.cz