Neomezený, a tedy na Zemi vždy jen dočasný exponenciální růst by se neměl zaměňovat (jak to někdy bývá) s hyperbolickým růstem. Zatímco exponenciální progres je charakterizován rostoucí absolutní rychlostí růstu, zůstává funkcí času, když se blíží nekonečnu; na rozdíl od toho hyperbolický růst vrcholí absurditou, protože množství roste směrem k …
více »Statistici vyvracejí nejčastější klišé spojená s tenisem
Proč může být lepší udělat více dvojchyb? Kam směřovat podání? Tenis je také hra, která se nejčastěji stává předmětem matematických rozborů, mezi nimiž vynikají práce dvou nizozemských statistiků – a výsledky jsou velmi zábavné. Franc Klaassen a Jan R. Magnus pracovali v Centru pro ekonomický výzkum na Tilburské univerzitě a …
více »Hra Othello skončí bez chyby remízou
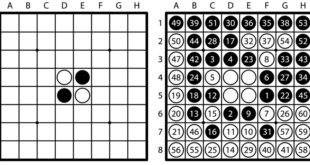
Othello (Reversi) je desková hra populární dnes především v Japonsku. Vznikla ovšem na konci 19. století v Anglii a její název se skutečně odvozuje od Shakespearova díla. Hraje v ní bílý proti černému na desce o rozměrech šachovnice (obdobná je pak i notace, viz obrázek), ovšem použité kameny mohou měnit …
více »Čeho se spíše bát? Blesku nebo pádu ze schodů?
Proč se někteří lidé bojí létání, když podle statistik jde snad o nejbezpečnější způsob dopravy? V rozmezí let 2002–2010 bylo ve Velké Británii při nehodách výtahů zraněno 266 lidí a čtyři osoby zemřely. Proč se tedy tak málo lidí bojí jezdit výtahem? Vždyť výtahy jsou v přepočtu na osobokilometr pravděpodobně …
více »Mince padá častěji tak, jak byla vyhozena
Možná je to výzkum hodný ocenění Ig Nobel, ale předpokládám, že autoři experimentu se při něm mohli dobře pobavit. Vědecký tým (výčet lidí podílejících se na studii zabítá 4 řádky) uskutečnil 350 757 hodů mincí (házelo 48 lidí ve 46 zemích). Cílem bylo otestovat spíše kontraintuitivní předpověď fyzikálního modelu „reálného“ …
více »Brunova konstanta a řada převrácených hodnot prvočíselných dvojic
Vzhledem k tomu, že součet převrácených hodnot všech prvočísel diverguje k nekonečnu, vypadá téměř neuvěřitelně, že součet prvočíselných dvojic konverguje… Viggo Brun (1885-1978) „Žádné odvětví teorie čísel není naplněno tolika záhadami jako studium prvočílel: oněch rozčilujících a vzpurných celých čísel, která odmítají být dělena beze zbytku jinými celými čísly kromě …
více »Horská dráha a Möbiova páska
Jízdu na horské dráze zbožňuju. Nejde mi ale jen o vzrušení. Jsem blázen do matematiky a vzrušuje mě všechna ta geometrie a kalkulus, jež se podílely na konstrukci atrakce, na níž je všechno napnuto na samý kraj možného, a souprava vozíků se přitom pevně drží v dráze. V Británii máme …
více »Sportovní sázení: skóre tipovat podle mediánu, nikoliv aritmetického průměru
Předpokládejme, že týmy Kansas City a Filadelfie spolu v této sezóně hrály dosud třikrát. Kansas City vyhrál každý z těchto zápasů, a to rozdílem 3, 7 a 35 bodů. Jak se postavit k možnosti, že Kansas City nyní vyhraje o 10 bodů, respektive při jakých kurzech sázet na koho? Nebo …
více »Poruchy motorů u elektromobilů dokážou odhalit matematické algoritmy
Najít poruchu elektromotoru není vždy snadné. K její efektivní diagnostice lze ale využít nové matematické algoritmy s parametrickým odhadem. Vývojem se několikátým rokem zabývá doktorand z FEKT VUT a výzkumník na CEITEC VUT Lukáš Zezula, který na svůj výzkum získal stipendium Brno Ph.D. Talent. Jeho algoritmy dokážou detekovat nejen přítomnost …
více »Analogový počítač z mýdlových bublin
Jedna z verzí známé úlohy obchodního cestujícího. Jak propojit několik měst sítí silnic tak, aby byla jejich délka co nejkratší? Pro ilustraci obtížnosti této úlohy se podívejme na „snadný“ případ, kdy máme propojit pouhá čtyři města A, B, C, D, která navíc šťastnou náhodou leží ve vrcholech čtverce o straně …
více » Sciencemag.cz
Sciencemag.cz