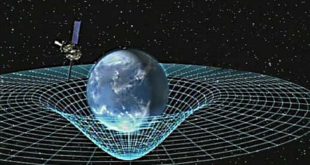
Vědci využili skutečně kuriózní metodu pro popis nástupu lidí do letadel – docela se prý hodí aplikovat matematiku z obecné teorie relativity. Jméno Lorentz známe především v souvislosti s příslušnou transformací, pomocí které se ve speciální teorii relativity přepočítávají při rychlostech blízkých rychlosti světla délky, časy a hmotnosti. (Příslušná matematika …
více »Matematika hudby a teorie relativity
Když Einstein formuloval obecnou relativitu, Schoenberg promýšlel nový systém komponování, který měl nahradit tonální systém. Na první pohled nemohli být ti dva muži rozdílnější: Arnold Schoenberg, nevysoký, s pleší na temeni, oči prozrazující nervózní napětí a rozrušení; Albert Einstein, o čtyři roky mladší, díky mohutné postavě a neupravené hřívě působící …
více »Co by bylo, kdyby – virtuální dějiny a letecká Bitva o Británii
Dřívější zahájení bojů i soustředění útoků na letiště by zvýšily pravděpodobnost porážky RAF. Virtuální dějiny, tedy úvahy a spekulace typu „co by, kdyby“, jsou rozhodně populární zábavou. Když se těmito úvahami zabývají historikové specializující se na danou událost, mělo by jít navíc o něco jiného než (jen) o sci-fi a …
více »Záhada husího hejna ve tvaru V: matematika v pozadí
Stěhovaví ptáci často létají ve formaci, která má tvar písmene V. Nejznámějším příkladem jsou hejna divokých hus ve tvaru V, která často čítají desítky nebo dokonce stovky ptáků. Co hejno nutí zaujmout tento tvar? Badatelé již dlouho předpokládají, že ve formaci tohoto tvaru se každý pták vyhýbá turbulentnímu vzduchovému víru …
více »Speciální sekvence projdou testy náhodnosti
Kryptografie, a to ani kvantová, se neobejde bez generátoru náhodných čísel. Pomiňme, zda náhodnost lze generovat jinak než kvantovou fyzikou, zapomeňme na rozdíl náhodnosti a pseudonáhodnosti. Nakonec pro použití v praxi je asi rozhodující test třetí strany – nějaké certifikační apod. autority. Vědci z izraelské Bar-Ilanovy univerzity nyní tvrdí, že …
více »Knihy roku: Tipy na vánoční dárky
Co doporučit z českého knižního trhu populárně-vědecké literatury? Co dát či si nechat dát pod stromeček? V letošním roce jsme se sice dočkali řady zajímavých titulů, u mnohých z nich se však jedná o dotisky či nová vydání. Tip č. 1 Marcus du Sautoy: Hudba prvočísel. Dvě století Riemannovy hypotézy …
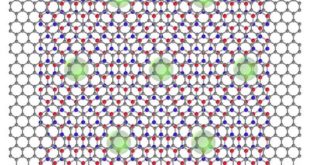
více »Démoni z Escherova obrazu odpovídají deformacím krystalů
Fascinující obrazy nizozemského malíře M. C. Eschera inspirují matematiky i fyziky od svého vzniku. Escherova díla souvisejí s takovými obory, jako je krystalografie či hyperbolická geometrie. Kresba Circle Limit IV (Heaven and Hell) představuje mozaikování pomocí obrazů andělů a démonů, které vyplňují kruh bez prázdných mezer. Paolo Biscari a jeho …
více »Násobíme pomocí prstů
V době raného středověku nebyl v Evropě všeobecně znám/používán abakus ani jiná podobná počítadla, neprováděly se zápisy průběhu výpočtu na papíře (pergamenu, tabulce…), a samozřejmě se nepoužívaly ani arabské číslice. Jak tedy lidé vůbec dokázali počítat? Používalo se především prstů a to nejen ke sčítání a odčítání, ale lidé s …
více »Věta o chlupaté kouli – matematika i pro nanodrátky
Pokud bude koule pokryta chlupy a my se je budeme snažit sčesat tak, aby všechny ležely hladce na ploše, vždy zůstane nejméně jeden vlas trčet, nebo vznikne holé místo. Rok 1912 Luitzen Egbertus Jan Brouwer (1881-1966) Badatel v oboru vědy o materiálech Francesco Stellacci z Massachusettského technologického institutu v roce …
více »Všechna pohoří si jsou podobná – matematicky
Prý nezávisí na absolutní výšce hor, na jejich stáří ani na tom, zda jsou tektonického nebo sopečného původu. Matematický popis všech dosud zkoumaných pozemských pohoří je obdobný, tvrdí alespoň vědci z Ústavu jaderné fyziky Polské akademie věd v Krakově. Jejich práce byla publikována v Journal of Complex Networks. Základem modelu …
více » Sciencemag.cz
Sciencemag.cz